Compte rendu réunion du 02.12.2020

Présentation “Joseph”

Descriptif : Direct-search methods for stochastic blackbox optimization

Résumé : Computational optimization is ubiquitous in many communities and has attracted an unparalleled interest during the last decades due to the growing use of computer simulations when solving complex problems arising in a plethora of fields, especially in engineering. Blackbox optimization (BBO), a major theme in the present thesis, does not assume the existence of derivatives and focuses on problems where the objective and constraint functions are given by a blackbox, typical examples of which are computer simulations. For many of such problems arising in machine learning, signal processing, medicine and biology to name a few, the target deterministic objective function and constraints can only be accessed through a blackbox corrupted by some random noise, thus resulting in stochastic BBO problems. Even though developing provable algorithms for stochastic optimization has recently received renewed interest, most of derivative-free optimization (DFO) methods either use estimated gradient informations, are restricted to unconstrained problems, or assume that the constraints are deterministic. Thus, direct-search methods known to be reliable and robust in practice appear to be the most promising approach for BBO problems. However in stochastic BBO, there is relatively scarce research on developing direct-search methods with full-supported convergence analysis especially when constraints function evaluations are also corrupted by some random noise. This thesis therefore focuses on the development and convergence analysis of direct-search methods for stochastic BBO.

The first project of this thesis introduces a stochastic extension of the mesh adaptive direct-search (MADS) algorithm originally designed for deterministic BBO. The proposed method called StoMADS considers the unconstrained optimization of an objective function when only having access to its noisy evaluations available through a blackbox corrupted by some random noise following an unknown distribution. Thus, since the exact deterministic values of the underlying objective function are not available, their estimates obtained from stochastic observations are used. By requiring the accuracy of such estimates to hold with a large but fixed probability and by assuming them to satisfy a variance condition, a Clarke stationarity convergence result of StoMADS is proved by means of martingale theory. Computational studies comparing StoMADS to algorithms available in the {\sf NOMAD} BBO software revealed that the proposed method is very promising for real-life applications.

The second project generalizes the algorithmic framework of StoMADS by introducing a broad class of stochastic directional direct-search (SDDS) algorithms which accept new iterates by imposing a sufficient decrease condition on function estimates required to satisfy the same StoMADS assumptions. By assuming in addition the objective function to be differentiable, the expected complexity of SDDS is analyzed making use of an existing supermartingale-based framework. Despite using no gradient information unlike prior methods such as stochastic line-search and stochastic trust-region methods, the convergence rate of SDDS is shown to be similar to that of both latter methods and to that of the broad class of deterministic directional direct-search methods which accept new iterates using a sufficient decrease condition.

By introducing the StoMADS-PB algorithm, the third project of the thesis focuses on the constrained stochastic BBO. The proposed method is a stochastic extension of the MADS method using a progressive barrier (PB) approach for constraints handling, originally developed for deterministic BBO under general constraints. Similarly to the framework of StoMADS, the objective and constraints function values can only be computed through a noisy blackbox. Constraints are treated by StoMADS-PB by aggregating their corresponding violations into a single {\it constraint violation function}. Since all the underlying deterministic functions values are not available, estimates are used and so-called {\it probabilistic bounds} are introduced for the violation function. By requiring such estimates and bounds to be accurate and reliable with sufficiently high but fixed probabilities, Clarke stationarity results for the objective and the violation function are derived with probability one, making use of the Clarke nonsmooth calculus and martingale theory. Numerical experiments conducted on 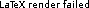stochastic variants of 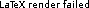constrained problems from literature demonstrated StoMADS-PB to outperform MADS with PB.

https://polymtl.webex.com/polymtl-en/j.php?MTID=ma3161729f9f22ed0fb54a6bf75a2f2b3

lieu : à distance

https://www.dropbox.com/sh/nd6fob8q8dnzwx5/AAAhRHzFH2d9NRBg8-hJhsI0a?dl=0